こんにちは!大手個別指導塾・現役教室長の大嶋です。
毎年受験シーズンになると
「Vもぎの偏差値が上がらない!どうすれば良いんですか!?」
という質問が後を絶ちません。
結論からお伝えします。
都立入試の数学は、誰でも簡単に偏差値60取れます。
これは私が、当時中学生として都立入試をこの身で経験し、現在は塾の先生として中学生たちに長く指導をしてきた経験から、断言できます。
そこで今回は、都立入試の数学で偏差値60を方法を紹介します。
数学の偏差値を上げたい全ての中学生にとって必見の内容です。
・都立入試の数学で偏差値60を取れる点数の目安
・どのような戦略で問題を解く必要があるのか
・問題を解けるようになるためには、どのような練習を積み重ねていく必要があるのか
数学は苦手意識を抱いている生徒さんが多いですが、僕と一緒に対策の仕方を確認していきましょう!
①まずは都立入試の数学の構造を理解しよう!

都立入試の攻略を始めるには、まずは敵を知るところから。
都立の数学は、毎年出る内容に大きな変化はありません。
具体的な構成は、以下の通り。
大問1(46点) 簡単な計算問題+作図
大問2(12点) 文字式+式の利用(証明)
大問3(15点) 関数(一次→二次→一次…と毎年交互に出題)
大問4(17点) 平面図形
大問5(10点) 空間図形(柱体→錐体→柱体…と毎年交互に出題)
学習指導要領に大きな変更がない限りは、これからもこの問題構成だと予想されます。
大問3の関数/大問5の立体は、毎年交互に出題内容が変わります。
自分の受験する年ではどっちが出題されるのか、チェックしておきましょう!
②偏差値60を取れる目安は80点程度

都立入試の数学では、80点程度取れていれば、偏差値60を取れます。
と、思いましたか?
しかし、都立入試の数学のレベルは決して高くないので、80点を取るのは難しくありません。
都立入試の問題は、一部の入試問題を自校作している高校を除いて、全てのレベルの中学生が受験するもの。
言い方は乱暴ですが、レベルの低い学校を受験する生徒さんも受ける問題なので、数学に限らず都立入試の問題の難易度は低めなのです。
80点と聞くとかなり高い点数に思えるかもしれません。
しかし実は、全然簡単に取れてしまうんです!
偏差値60に到達するためには80点程度必要。
でも都立入試は難易度が低いから、決して難しくない。
③解かない問題・絶対に正解する問題を分けよう
80点取ることを目標にしたら「どの問題を解かないのか」を決めましょう。
80点が目標なのに、100点満点を取るために頑張るのは、効率が悪いから。
都立入試の場合、80点で良いのであれば、解く問題を4問減らせます。
50分しかない試験本番で、4問も解く問題を減らせるのは、かなり余裕が生まれます。
どの問題を確実に解き、どの問題を捨てるのか…
私が普段塾生たちにオススメしている解き方は以下の通りです。
大問1 完答(46点)
大問2 完答(12点)
大問3 最後の問題以外(10点)
大問4 最後の問題以外(12点)
大問5 解かないor問1のみ回答(0〜5点)
合計:80〜85点
大問2の証明問題は、かなり苦手意識を持っている生徒さんが多いです。
しかし、この問題ほど「練習量で解けるようになる」問題はありません。
また、大問5は①を解けば85点満点。解かずに他の問題に時間を回せばより確実に80点を狙えます。
ただ、大問1全て、3と4の最後の問題以外は、難易度がかなり低いので確実に正解しなければなりません。
これらの問題は、間違えた瞬間に「偏差値60は絶対取れない」と思った方が良いです。
④都立入試数学の各大問の対策方法は?

都立入試の数学で偏差値60を取るために、言えることは
「とにかく基礎的な内容を完璧にしよう!」
これです。
特に、80点を取るだけなら、応用問題は1問も解けなくて良いレベル。
その上で、各大問に関する詳しい対策の仕方を、紹介します。
大問1 小問集合

ここでは、基本的な計算など、超簡単な問題ばかり出題されます。
出題範囲は、以下の通り。
【必出】
・四則演算
・文字式
・平方根
・一次方程式
・二次方程式
・連立方程式
・作図
【2問ランダムで出題】
・関数
・確率
・資料の活用
・角度
一見すると、かなり範囲が広いように思えます。
ただどの問題も、超基本中の基本レベルなのでかなり簡単。
入試やVもぎ・Wもぎの過去問、その他都立特化の問題集で練習していれば、確実に満点を取れます。
それにもかかわらず、配点が46点とかなり高いです。
そのため、偏差値60を取りたいなら、確実に満点を取らなければなりません。
大問2 式の利用
大問2の出題範囲は以下の通り。
・文字式
・式の利用
問1

与えられた条件に従って、文字式で答える問題が出題されます。
図形に関する理解と法則性へのひらめきのどちらかが聞かれることがほとんど。
どちらの問題を解くにしても、特別難しい知識は必要ありません。
法則性の問題は、ひらめきが要求されることがほとんど。
しかし、もし法則がわからなくても、無理矢理計算すれば答えを出せます。
そのため、諦めずに計算すれば、必ず得点できるのです。
問2
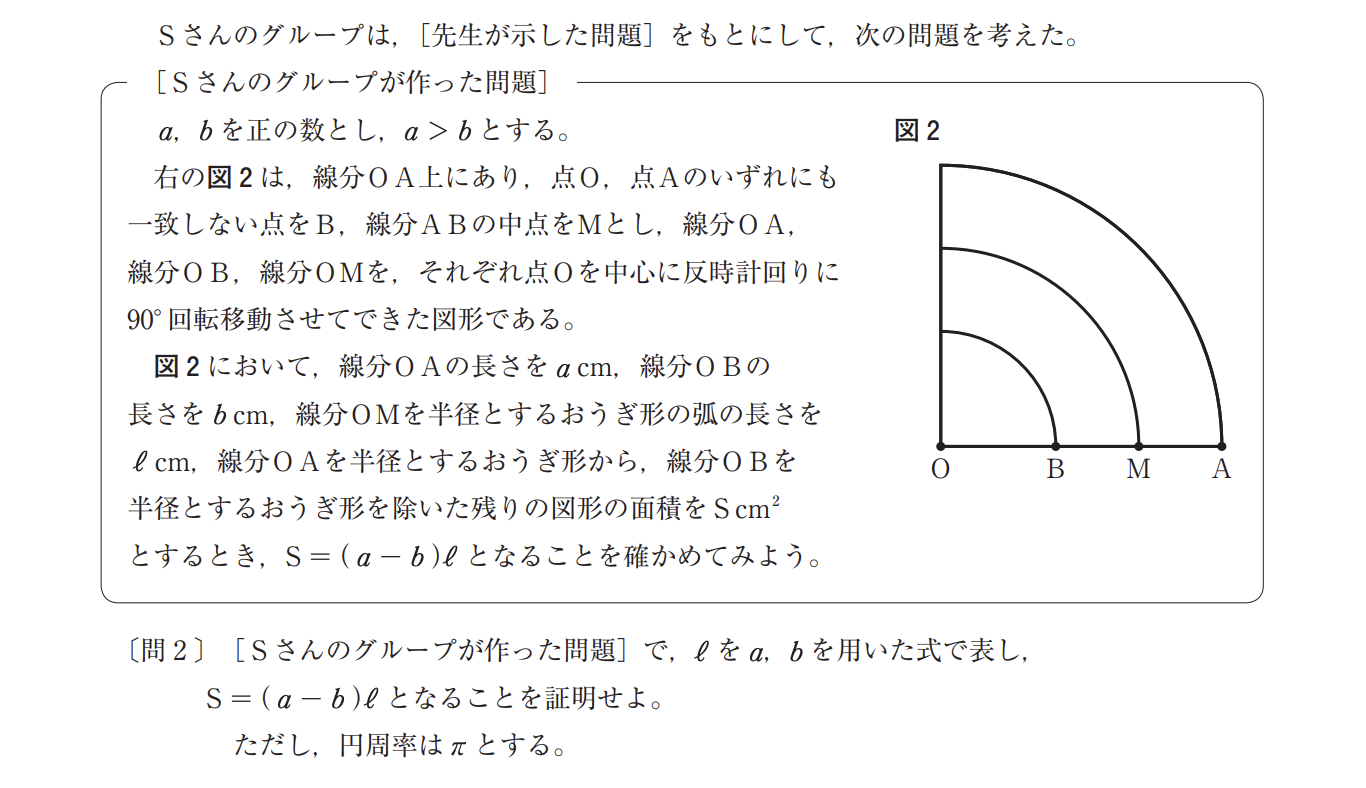
ここでは、文字式を使った証明問題が出題されます。
「難しいことを知っているか」よりも「数学的思考力」が問われている問題です。
何度も練習を繰り返して、この問題を解く思考力や、勘を養うことが一番の対策になります。
該当単元は、2年生の『式の計算』3年生の『多項式の計算』です。
入試・Vもぎ・Wもぎの過去問、都立入試特化問題集で、練習を繰り返すのがおすすめ。
大問3 関数
問1
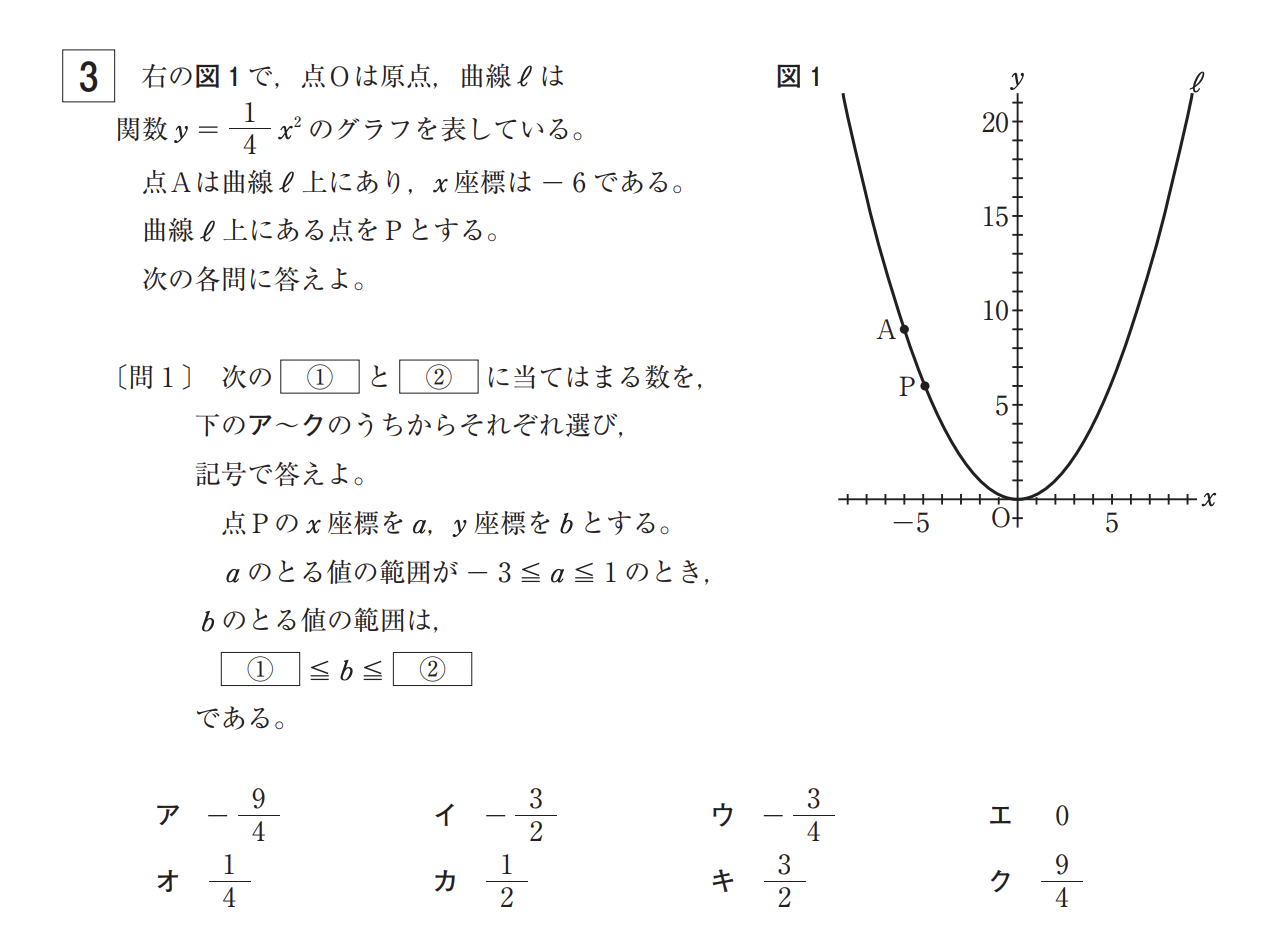
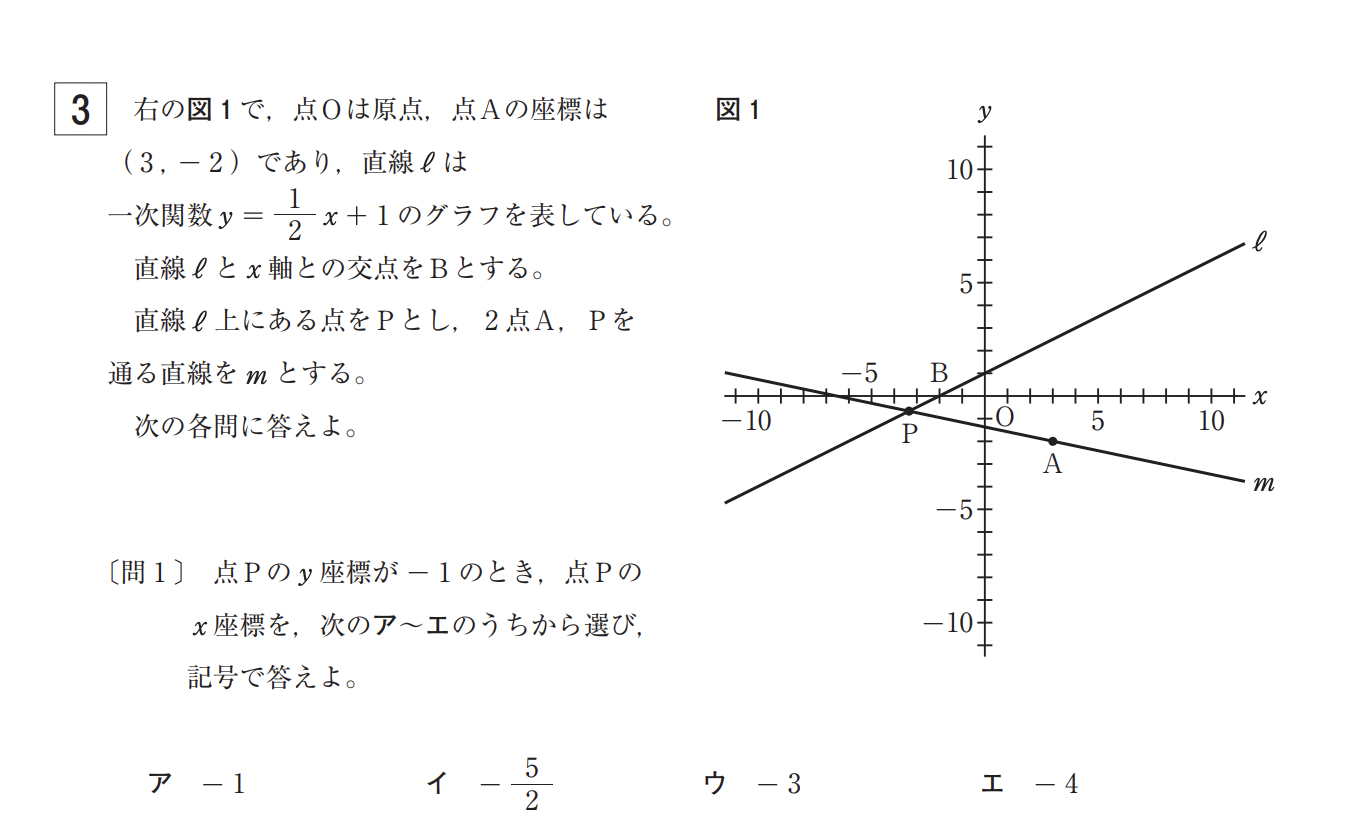
ここで問われる問題は、以下の通り。
一次関数:ある点について、片方の座標が分かっている状態で、もう片方の座標を求める問題
二次関数:x変域が分かっている状態で、yの変域を求める問題
超簡単なんです。
正直、習いたての人でも簡単に正解できるレベル。
超基本中の基本問題、ということです。
学校のワークでも良いので、超基本問題を確実にできるようにすれば、確実に得点できるようになります。
上記の一次関数の問題は、l(エル)の式に「y=3」を代入すればOK(答えは”ウ”)。
二次関数問題は、シンプルにxの変域が「-3≦x≦1」のときのyの変域を求めればOK(答えは①がエ、②がク)。
問2 ①
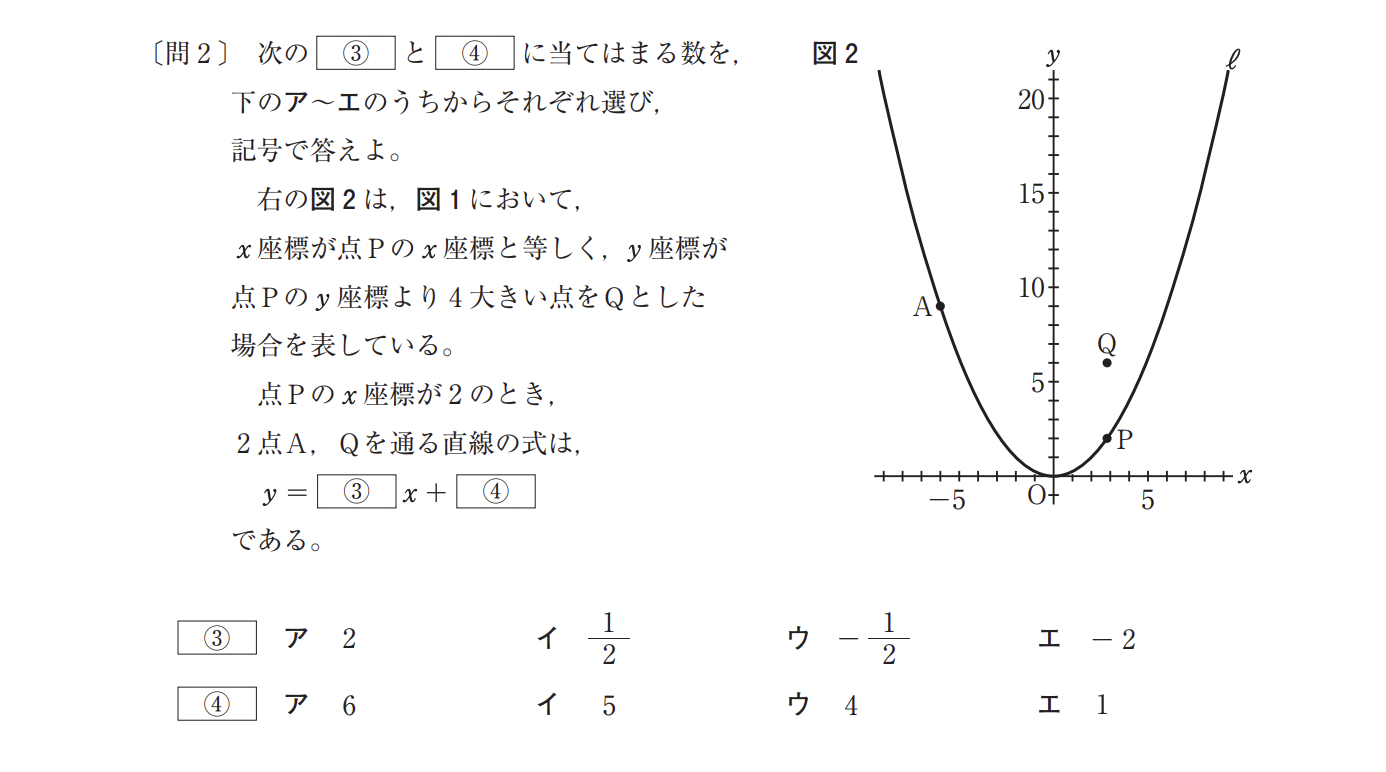

問2の①は一見すると難しそうです。
しかし、ゆっくり落ち着いて図の中にメモを取って、養ってきた基礎力を発揮すれば、全く難しくありません。
上記、二次関数の問題は、Pの座標が(2,1)です。
そのため、Pよりy座標が4大きいQの座標は(2,5)となります。
A(-6,9)Q(2,5)を通る直線の式を求めれば良いので…
答えは③はウ、④はアだとわかります。
一次関数の問題は、y軸がBPの二等分線なので、BPとy軸の交点が中点になることがわかります。
BPとy軸の交点は、直線l(エル)とy軸の交点と同じなので(0,1)となる。
Bから(0,1)までは、右に2つ・上に1つ進んでいるので、Pの座標は(0,1)から右に2つ、上に1つ進んだ位置、すなわち(2,2)となる。
直線mは、A(3,-2)と(2.2)が通る直線なので、その直線の指揮を求めれば良い。
したがって①はイ、②はエだとわかります。
難しそうに見えて、さほど難しくありません。
ただこれらの問題は「基本問題が解ける」だけでは、解けるようになりません。
関数の基本事項を「理解している」必要があります。
「理解しているかどうか」の基準は「友達に解説できるかどうか」です。
もし「問題は解けるけど、友達にうまく説明できない」問題があったら、それは理解できていない証拠。必ず理解を深めて、説明できるようにしましょう。
大問4 平面図形
問1

角度の大きさを、文字を使って答える問題です。
この問題では、角度の基礎知識を漏れなく運用出来るか、が問われています。
難しいことは全く聞かれません。
ただ、簡単な知識を使いこなせないと、中々正解に辿り着けません。
コツは「分かった情報は、図形に全部書き込む」こと。
分かった角度の大きさ、辺の長さ関係など、とにかく図形にメモしまくりましょう。
そうしていると「そういうことか!」と答えに辿りつけるようになります。
問2 ①
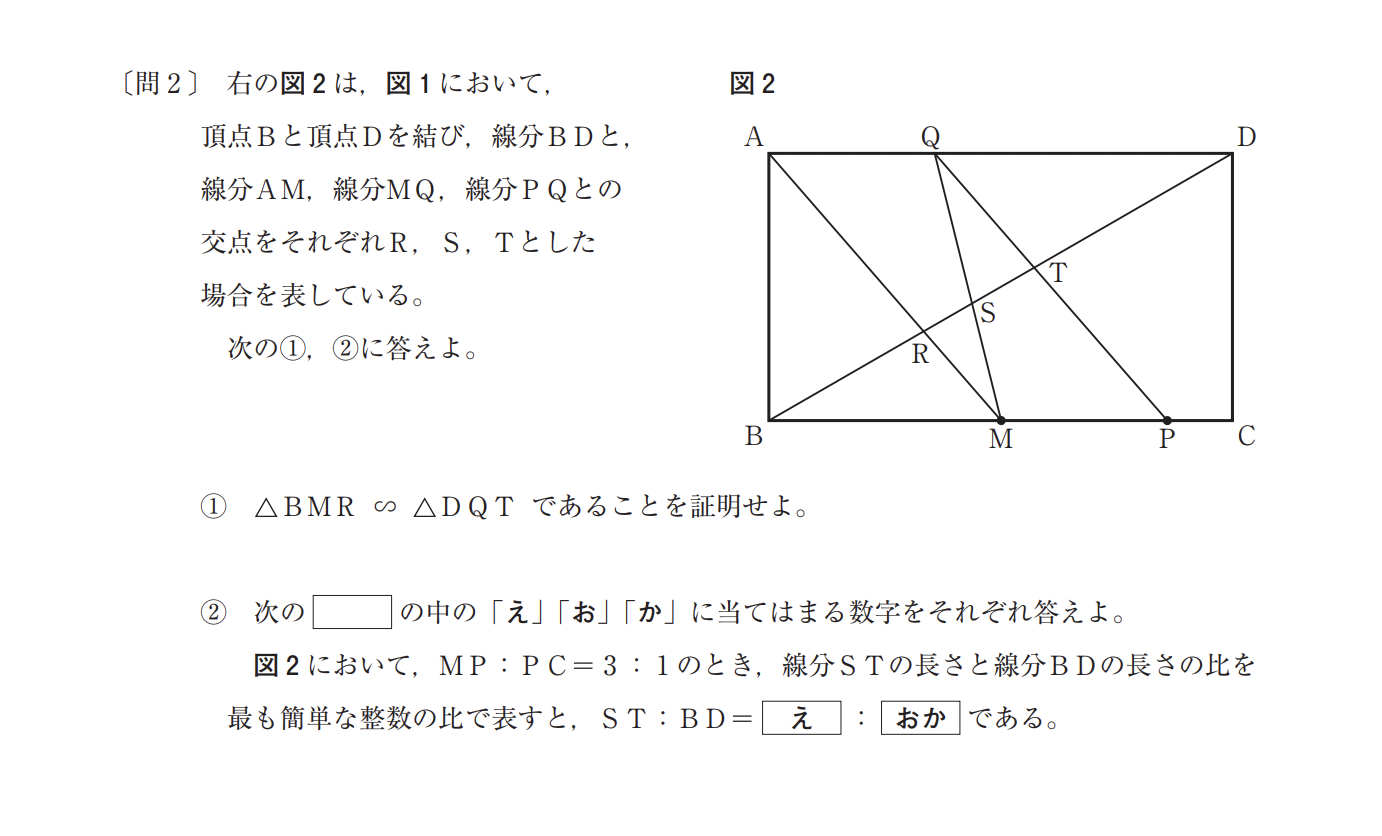
ここでは、合同か相似の証明が出題されます。
これが驚くほど簡単なんです。
証明が超得意ではなくても解けてしまうレベルのものが、毎年出題されています。
しかし、「そんな壁を貼っているのは本当にもったいない!」
と叫びたくなるレベルで、都立数学の証明は簡単なのです。
合同や相似の証明が苦手な生徒さんのほとんどは
という激しい思い込みと、単なる演習不足が原因。
都立入試の証明で使う知識自体は、とても簡単なものばかり。
平面図形に関する知識を漏れなくインプットして、苦手意識を持たずに、練習問題に挑戦しましょう。
問題集の応用問題が解けなくても、都立入試はOK!
とにかく、基礎的な証明は必ずできるようにしよう!
大問5 空間図形 問1
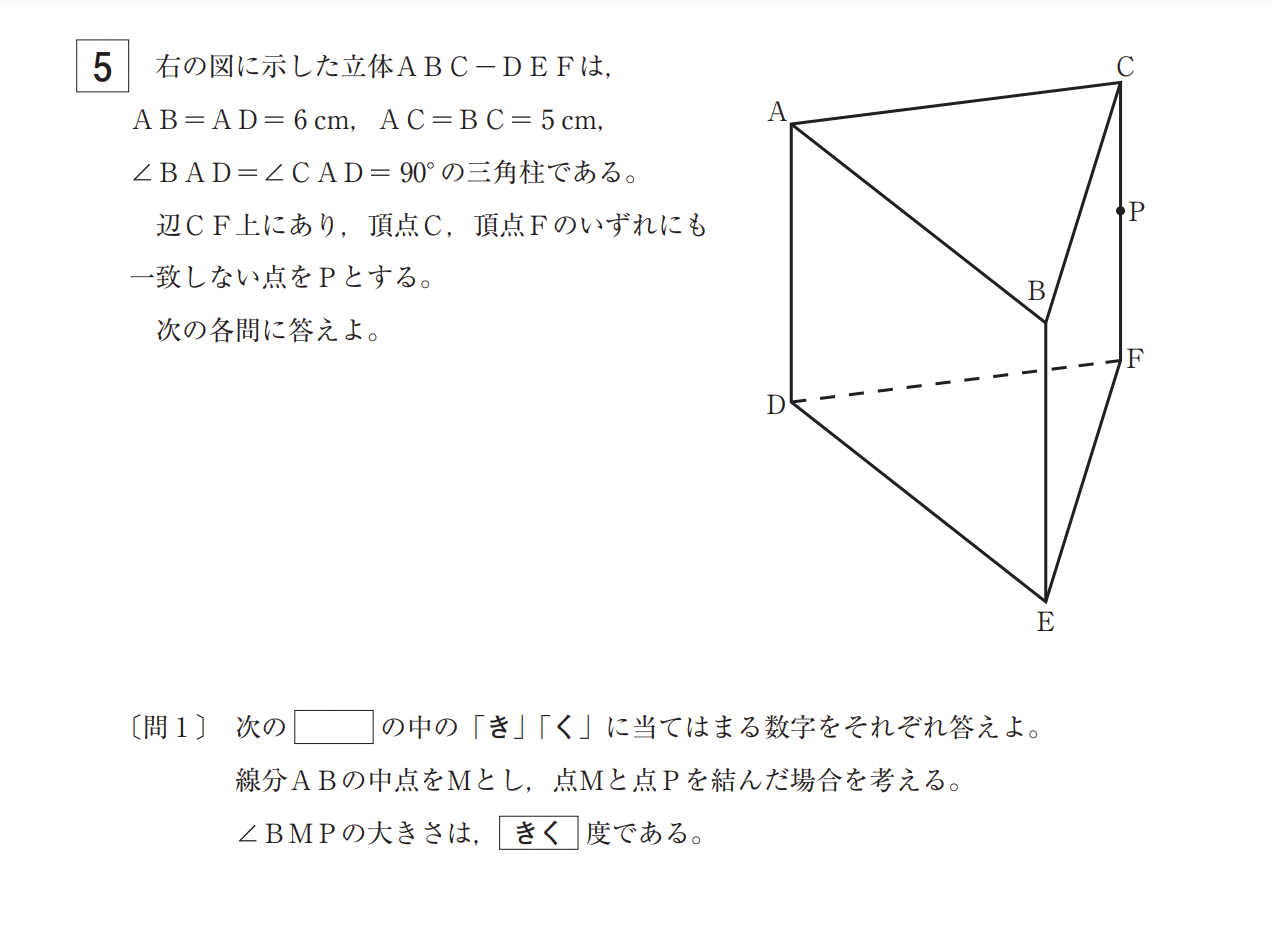
柱体や錐体の角度の大きさ・辺の長さ・面積・面積比などを求める問題が出題されます。
この問題は、3年生の後半で習う相似や三平方の定理を使うため、本格的な対策を打ち始めるタイミングが遅め。
そのため、多くの生徒さんが強烈な苦手意識を抱いている問題です。
とは言っても、大問5は都立入試の中でもトップクラスの難易度の高さを誇ります。
そのため、過去問や都立対策問題集に何度も挑戦して、解説を熟読するのが、おすすめの勉強方法です。
ちなみに、角度の問題に関してはこれまで答えが「60度」「90度」の2つしかありませんでした。
そのため、角度の問題で迷ったらどちらかを選んでおくと正解するかもしれません。
最終手段として覚えておくことを、おすすめします。
最後に

今回は、都立入試の数学で偏差値60に到達する方法を紹介しました。
今回の内容をまとめると以下の通り。
・偏差値60に到達するには80点くらい取れば良い
・とにかく基礎の徹底をし、友達に説明できるくらいに理解しておくことが大切
・難しい応用問題は無視してOK!
とにかく数学は、過去問を中心に練習を繰り返すことが重要!
まだ過去問を買っていない人は、今すぐ買っておきましょう!